Tutorial
Trie Data Structure in C/C++

While we believe that this content benefits our community, we have not yet thoroughly reviewed it. If you have any suggestions for improvements, please let us know by clicking the “report an issue“ button at the bottom of the tutorial.
A Trie data structure acts as a container for a dynamic array. In this article, we shall look at how we can implement a Trie in C/C++.
This is based on the tree data structure but does not necessarily store keys. Here, each node only has a value, which is defined based on the position.
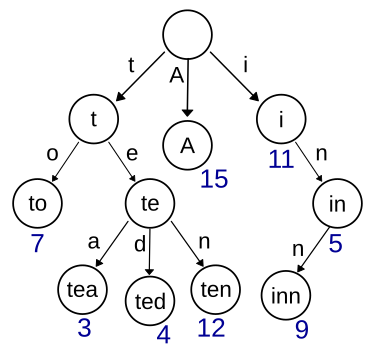
So, the value of each node denotes the prefix, because it is the point from the root node after a series of matches.
We call such matches as prefix matches. Therefore, we can use Tries to store words of a dictionary!
For example, in the above figure, the root node is empty, so every string matches the root node. Node 7 matches a prefix string of to, while node 3 matches a prefix string of tea.
Here, the keys are only stored in the leaf node positions, since prefix matching stops at any leaf node. So any non-leaf node does NOT store the whole string, but only the prefix match character.
Tries are called prefix trees for all these reasons. Now let’s understand how we can implement this data structure, from a programmer’s point of view.
Implementing a Trie Data Structure in C/C++
Let’s first write down the Trie structure. A Trie Node has notably two components:
- It’s children
- A marker to indicate a leaf node.
But, since we’ll be printing the Trie too, it will be easier if we can store one more attribute in the data part.
So let’s define the TrieNode structure. Here, since I will be storing only the lower case alphabets, I will implement this as a 26-ary-tree. So, each node will have pointers to 26 children.
// The number of children for each node
// We will construct a N-ary tree and make it
// a Trie
// Since we have 26 english letters, we need
// 26 children per node
#define N 26
typedef struct TrieNode TrieNode;
struct TrieNode {
// The Trie Node Structure
// Each node has N children, starting from the root
// and a flag to check if it's a leaf node
char data; // Storing for printing purposes only
TrieNode* children[N];
int is_leaf;
};
Now that we’ve defined our structure, let’s write functions to initialize a TrieNode in memory, and also to free it’s pointer.
TrieNode* make_trienode(char data) {
// Allocate memory for a TrieNode
TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
for (int i=0; i<N; i++)
node->children[i] = NULL;
node->is_leaf = 0;
node->data = data;
return node;
}
void free_trienode(TrieNode* node) {
// Free the trienode sequence
for(int i=0; i<N; i++) {
if (node->children[i] != NULL) {
free_trienode(node->children[i]);
}
else {
continue;
}
}
free(node);
}
Inserting a word onto the Trie
We’ll now write the insert_trie() function, that takes a pointer to the root node (topmost node) and inserts a word to the Trie.
The insertion procedure is simple. It iterates through the word character by character and evaluates the relative position.
For example, a character of b will have a position of 1, so will be the second child.
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
We will match the prefix character by character, and simply initialize a node if it doesn’t exist.
Otherwise, we simply keep moving down the chain, until we have matched all the characters.
temp = temp->children[idx];
Finally, we will have inserted all unmatched characters, and we will return back the updated Trie.
TrieNode* insert_trie(TrieNode* root, char* word) {
// Inserts the word onto the Trie
// ASSUMPTION: The word only has lower case characters
TrieNode* temp = root;
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
// Go down a level, to the child referenced by idx
// since we have a prefix match
temp = temp->children[idx];
}
// At the end of the word, mark this node as the leaf node
temp->is_leaf = 1;
return root;
}
Search for a word in the Trie
Now that we’ve implemented insertion onto a Trie, let’s look at searching for a given pattern.
We’ll try to match the string character by character, using the same prefix matching strategy as above.
If we have reached the end of the chain and haven’t yet found a match, that means that the string does not exist, as a complete prefix match is not done.
For this to return correctly, our pattern must exactly match, and after we finish matching, we must reach a leaf node.
int search_trie(TrieNode* root, char* word)
{
// Searches for word in the Trie
TrieNode* temp = root;
for(int i=0; word[i]!='\0'; i++)
{
int position = word[i] - 'a';
if (temp->children[position] == NULL)
return 0;
temp = temp->children[position];
}
if (temp != NULL && temp->is_leaf == 1)
return 1;
return 0;
}
Okay, so we’ve completed the insert and search procedures.
To test it, we’ll first write a print_tree() function, that prints the data of every node.
void print_trie(TrieNode* root) {
// Prints the nodes of the trie
if (!root)
return;
TrieNode* temp = root;
printf("%c -> ", temp->data);
for (int i=0; i<N; i++) {
print_trie(temp->children[i]);
}
}
Now that we have done that, let’s just run the complete program until now, to check that it’s working correctly.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// The number of children for each node
// We will construct a N-ary tree and make it
// a Trie
// Since we have 26 english letters, we need
// 26 children per node
#define N 26
typedef struct TrieNode TrieNode;
struct TrieNode {
// The Trie Node Structure
// Each node has N children, starting from the root
// and a flag to check if it's a leaf node
char data; // Storing for printing purposes only
TrieNode* children[N];
int is_leaf;
};
TrieNode* make_trienode(char data) {
// Allocate memory for a TrieNode
TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
for (int i=0; i<N; i++)
node->children[i] = NULL;
node->is_leaf = 0;
node->data = data;
return node;
}
void free_trienode(TrieNode* node) {
// Free the trienode sequence
for(int i=0; i<N; i++) {
if (node->children[i] != NULL) {
free_trienode(node->children[i]);
}
else {
continue;
}
}
free(node);
}
TrieNode* insert_trie(TrieNode* root, char* word) {
// Inserts the word onto the Trie
// ASSUMPTION: The word only has lower case characters
TrieNode* temp = root;
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
// Go down a level, to the child referenced by idx
// since we have a prefix match
temp = temp->children[idx];
}
// At the end of the word, mark this node as the leaf node
temp->is_leaf = 1;
return root;
}
int search_trie(TrieNode* root, char* word)
{
// Searches for word in the Trie
TrieNode* temp = root;
for(int i=0; word[i]!='\0'; i++)
{
int position = word[i] - 'a';
if (temp->children[position] == NULL)
return 0;
temp = temp->children[position];
}
if (temp != NULL && temp->is_leaf == 1)
return 1;
return 0;
}
void print_trie(TrieNode* root) {
// Prints the nodes of the trie
if (!root)
return;
TrieNode* temp = root;
printf("%c -> ", temp->data);
for (int i=0; i<N; i++) {
print_trie(temp->children[i]);
}
}
void print_search(TrieNode* root, char* word) {
printf("Searching for %s: ", word);
if (search_trie(root, word) == 0)
printf("Not Found\n");
else
printf("Found!\n");
}
int main() {
// Driver program for the Trie Data Structure Operations
TrieNode* root = make_trienode('\0');
root = insert_trie(root, "hello");
root = insert_trie(root, "hi");
root = insert_trie(root, "teabag");
root = insert_trie(root, "teacan");
print_search(root, "tea");
print_search(root, "teabag");
print_search(root, "teacan");
print_search(root, "hi");
print_search(root, "hey");
print_search(root, "hello");
print_trie(root);
free_trienode(root);
return 0;
}
After compiling with your gcc compiler, you’ll get the following output.
Searching for tea: Not Found
Searching for teabag: Found!
Searching for teacan: Found!
Searching for hi: Found!
Searching for hey: Not Found
Searching for hello: Found!
-> h -> e -> l -> l -> o -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->
While it may be obvious how it’s being printed, the clue is to look at the print_tree() method. Since that prints the current node, and then all of its children, the order does indicate that.
So, now let’s implement the delete method!
Delete a word from a Trie
This one is actually a bit more tricky than the other two methods.
There doesn’t exist any format algorithm of sorts since there is no explicit way in which we store the keys and values.
But, for the purpose of this article, I’ll handle deletions only if the word to be deleted is a leaf node. That is, it must be prefix matched all the way, until a leaf node.
So let’s start. Our signature for the delete function will be:
TrieNode* delete_trie(TrieNode* root, char* word);
As mentioned earlier, this will delete only if the prefix match is done until a leaf node. So let’s write another function is_leaf_node(), that does this for us.
int is_leaf_node(TrieNode* root, char* word) {
// Checks if the prefix match of word and root
// is a leaf node
TrieNode* temp = root;
for (int i=0; word[i]; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
temp = temp->children[position];
}
}
return temp->is_leaf;
}
Okay, so with that completed, let’s look at the draft of our delete_trie() method.
TrieNode* delete_trie(TrieNode* root, char* word) {
// Will try to delete the word sequence from the Trie only it
// ends up in a leaf node
if (!root)
return NULL;
if (!word || word[0] == '\0')
return root;
// If the node corresponding to the match is not a leaf node,
// we stop
if (!is_leaf_node(root, word)) {
return root;
}
// TODO
}
After this check is done, we now know that our word will end in a leaf node.
But there is another situation to handle. What if there exists another word that has a partial prefix match of the current string?
For example, in the below Trie, the words tea and ted have a partial common match until te.

So, if this happens, we cannot simply delete the whole sequence from t to a, as then, both the chains will be deleted, as they are linked!
Therefore, we need to find the deepest point until which such matches occur. Only after that, can we delete the remaining chain.
This involves finding the longest prefix string, so let’s write another function.
char* longest_prefix(TrieNode* root, char* word);
This will return the longest match in the Trie, which is not the current word (word). The below code explains every intermediate step in the comments.
char* find_longest_prefix(TrieNode* root, char* word) {
// Finds the longest common prefix substring of word
// in the Trie
if (!word || word[0] == '\0')
return NULL;
// Length of the longest prefix
int len = strlen(word);
// We initially set the longest prefix as the word itself,
// and try to back-track from the deepest position to
// a point of divergence, if it exists
char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
for (int i=0; word[i] != '\0'; i++)
longest_prefix[i] = word[i];
longest_prefix[len] = '\0';
// If there is no branching from the root, this
// means that we're matching the original string!
// This is not what we want!
int branch_idx = check_divergence(root, longest_prefix) - 1;
if (branch_idx >= 0) {
// There is branching, We must update the position
// to the longest match and update the longest prefix
// by the branch index length
longest_prefix[branch_idx] = '\0';
longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
}
return longest_prefix;
}
There is another twist here! Since we try to find the longest match, the algorithm will actually greedily match the original string itself! This is not what we want.
We want the longest match that is NOT the input string. So, we must have a check with another method check_divergence().
This will check if there is any branching from the root to the current position, and return the length of the best match which is NOT the input.
If we are in the bad chain, that corresponds to the original string, then there will be no branching from the point! So this is a good way for us to avoid that nasty point, using check_divergence().
int check_divergence(TrieNode* root, char* word) {
// Checks if there is branching at the last character of word
//and returns the largest position in the word where branching occurs
TrieNode* temp = root;
int len = strlen(word);
if (len == 0)
return 0;
// We will return the largest index where branching occurs
int last_index = 0;
for (int i=0; i < len; i++) {
int position = word[i] - 'a';
if (temp->children[position]) {
// If a child exists at that position
// we will check if there exists any other child
// so that branching occurs
for (int j=0; j<N; j++) {
if (j != position && temp->children[j]) {
// We've found another child! This is a branch.
// Update the branch position
last_index = i + 1;
break;
}
}
// Go to the next child in the sequence
temp = temp->children[position];
}
}
return last_index;
}
Finally, we’ve ensured that we don’t just delete the whole chain blindly. So now let’s move on with our delete method.
TrieNode* delete_trie(TrieNode* root, char* word) {
// Will try to delete the word sequence from the Trie only it
// ends up in a leaf node
if (!root)
return NULL;
if (!word || word[0] == '\0')
return root;
// If the node corresponding to the match is not a leaf node,
// we stop
if (!is_leaf_node(root, word)) {
return root;
}
TrieNode* temp = root;
// Find the longest prefix string that is not the current word
char* longest_prefix = find_longest_prefix(root, word);
//printf("Longest Prefix = %s\n", longest_prefix);
if (longest_prefix[0] == '\0') {
free(longest_prefix);
return root;
}
// Keep track of position in the Trie
int i;
for (i=0; longest_prefix[i] != '\0'; i++) {
int position = (int) longest_prefix[i] - 'a';
if (temp->children[position] != NULL) {
// Keep moving to the deepest node in the common prefix
temp = temp->children[position];
}
else {
// There is no such node. Simply return.
free(longest_prefix);
return root;
}
}
// Now, we have reached the deepest common node between
// the two strings. We need to delete the sequence
// corresponding to word
int len = strlen(word);
for (; i < len; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
// Delete the remaining sequence
TrieNode* rm_node = temp->children[position];
temp->children[position] = NULL;
free_trienode(rm_node);
}
}
free(longest_prefix);
return root;
}
The above code simply finds the deepest node for the prefix match and deletes the remaining sequence matching word from the Trie, since that is independent of any other match.
Time Complexity for the above Procedures
The Time Complexity of the procedures are mentioned below.
| Procedure | Time Complexity of Implementation |
search_trie() |
O(n) -> n is the length of the input string |
insert_trie() |
O(n) -> n is the length of the input string |
delete_trie() |
O(C*n) -> C is the number of alphabets, |
| n is the length of the input word |
For almost all cases, the number of alphabets is a constant, so the complexity of delete_trie() is also reduced to O(n).
The Complete C/C++ program for the Trie Data Structure
At long last, we’ve (hopefully), completed our delete_trie() function. Let’s check if what we’ve written was correct, using our driver program.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// The number of children for each node
// We will construct a N-ary tree and make it
// a Trie
// Since we have 26 english letters, we need
// 26 children per node
#define N 26
typedef struct TrieNode TrieNode;
struct TrieNode {
// The Trie Node Structure
// Each node has N children, starting from the root
// and a flag to check if it's a leaf node
char data; // Storing for printing purposes only
TrieNode* children[N];
int is_leaf;
};
TrieNode* make_trienode(char data) {
// Allocate memory for a TrieNode
TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
for (int i=0; i<N; i++)
node->children[i] = NULL;
node->is_leaf = 0;
node->data = data;
return node;
}
void free_trienode(TrieNode* node) {
// Free the trienode sequence
for(int i=0; i<N; i++) {
if (node->children[i] != NULL) {
free_trienode(node->children[i]);
}
else {
continue;
}
}
free(node);
}
TrieNode* insert_trie(TrieNode* root, char* word) {
// Inserts the word onto the Trie
// ASSUMPTION: The word only has lower case characters
TrieNode* temp = root;
for (int i=0; word[i] != '\0'; i++) {
// Get the relative position in the alphabet list
int idx = (int) word[i] - 'a';
if (temp->children[idx] == NULL) {
// If the corresponding child doesn't exist,
// simply create that child!
temp->children[idx] = make_trienode(word[i]);
}
else {
// Do nothing. The node already exists
}
// Go down a level, to the child referenced by idx
// since we have a prefix match
temp = temp->children[idx];
}
// At the end of the word, mark this node as the leaf node
temp->is_leaf = 1;
return root;
}
int search_trie(TrieNode* root, char* word)
{
// Searches for word in the Trie
TrieNode* temp = root;
for(int i=0; word[i]!='\0'; i++)
{
int position = word[i] - 'a';
if (temp->children[position] == NULL)
return 0;
temp = temp->children[position];
}
if (temp != NULL && temp->is_leaf == 1)
return 1;
return 0;
}
int check_divergence(TrieNode* root, char* word) {
// Checks if there is branching at the last character of word
// and returns the largest position in the word where branching occurs
TrieNode* temp = root;
int len = strlen(word);
if (len == 0)
return 0;
// We will return the largest index where branching occurs
int last_index = 0;
for (int i=0; i < len; i++) {
int position = word[i] - 'a';
if (temp->children[position]) {
// If a child exists at that position
// we will check if there exists any other child
// so that branching occurs
for (int j=0; j<N; j++) {
if (j != position && temp->children[j]) {
// We've found another child! This is a branch.
// Update the branch position
last_index = i + 1;
break;
}
}
// Go to the next child in the sequence
temp = temp->children[position];
}
}
return last_index;
}
char* find_longest_prefix(TrieNode* root, char* word) {
// Finds the longest common prefix substring of word
// in the Trie
if (!word || word[0] == '\0')
return NULL;
// Length of the longest prefix
int len = strlen(word);
// We initially set the longest prefix as the word itself,
// and try to back-tracking from the deepst position to
// a point of divergence, if it exists
char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
for (int i=0; word[i] != '\0'; i++)
longest_prefix[i] = word[i];
longest_prefix[len] = '\0';
// If there is no branching from the root, this
// means that we're matching the original string!
// This is not what we want!
int branch_idx = check_divergence(root, longest_prefix) - 1;
if (branch_idx >= 0) {
// There is branching, We must update the position
// to the longest match and update the longest prefix
// by the branch index length
longest_prefix[branch_idx] = '\0';
longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
}
return longest_prefix;
}
int is_leaf_node(TrieNode* root, char* word) {
// Checks if the prefix match of word and root
// is a leaf node
TrieNode* temp = root;
for (int i=0; word[i]; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
temp = temp->children[position];
}
}
return temp->is_leaf;
}
TrieNode* delete_trie(TrieNode* root, char* word) {
// Will try to delete the word sequence from the Trie only it
// ends up in a leaf node
if (!root)
return NULL;
if (!word || word[0] == '\0')
return root;
// If the node corresponding to the match is not a leaf node,
// we stop
if (!is_leaf_node(root, word)) {
return root;
}
TrieNode* temp = root;
// Find the longest prefix string that is not the current word
char* longest_prefix = find_longest_prefix(root, word);
//printf("Longest Prefix = %s\n", longest_prefix);
if (longest_prefix[0] == '\0') {
free(longest_prefix);
return root;
}
// Keep track of position in the Trie
int i;
for (i=0; longest_prefix[i] != '\0'; i++) {
int position = (int) longest_prefix[i] - 'a';
if (temp->children[position] != NULL) {
// Keep moving to the deepest node in the common prefix
temp = temp->children[position];
}
else {
// There is no such node. Simply return.
free(longest_prefix);
return root;
}
}
// Now, we have reached the deepest common node between
// the two strings. We need to delete the sequence
// corresponding to word
int len = strlen(word);
for (; i < len; i++) {
int position = (int) word[i] - 'a';
if (temp->children[position]) {
// Delete the remaining sequence
TrieNode* rm_node = temp->children[position];
temp->children[position] = NULL;
free_trienode(rm_node);
}
}
free(longest_prefix);
return root;
}
void print_trie(TrieNode* root) {
// Prints the nodes of the trie
if (!root)
return;
TrieNode* temp = root;
printf("%c -> ", temp->data);
for (int i=0; i<N; i++) {
print_trie(temp->children[i]);
}
}
void print_search(TrieNode* root, char* word) {
printf("Searching for %s: ", word);
if (search_trie(root, word) == 0)
printf("Not Found\n");
else
printf("Found!\n");
}
int main() {
// Driver program for the Trie Data Structure Operations
TrieNode* root = make_trienode('\0');
root = insert_trie(root, "hello");
root = insert_trie(root, "hi");
root = insert_trie(root, "teabag");
root = insert_trie(root, "teacan");
print_search(root, "tea");
print_search(root, "teabag");
print_search(root, "teacan");
print_search(root, "hi");
print_search(root, "hey");
print_search(root, "hello");
print_trie(root);
printf("\n");
root = delete_trie(root, "hello");
printf("After deleting 'hello'...\n");
print_trie(root);
printf("\n");
root = delete_trie(root, "teacan");
printf("After deleting 'teacan'...\n");
print_trie(root);
printf("\n");
free_trienode(root);
return 0;
}
Output
Searching for tea: Not Found
Searching for teabag: Found!
Searching for teacan: Found!
Searching for hi: Found!
Searching for hey: Not Found
Searching for hello: Found!
-> h -> e -> l -> l -> o -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->
After deleting 'hello'...
-> h -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->
After deleting 'teacan'...
-> h -> i -> t -> e -> a -> b -> a -> g ->
With that, we’ve come to the end of our Trie Data Structure implementation in C/C++. I know that this is a long read, but hopefully you’ve understood how you can apply these methods correctly!
Download the Code
You can find the complete code in a Github Gist that I’ve uploaded. It may not be the most efficient code, but I’ve tried my best to ensure that it’s working correctly.
If you have any questions or suggestions, do raise them in the comment section below!
References
Recommended Reads:
If you’re interested in similar topics, you can refer to the Data Structures and Algorithms section, which includes topics like Hash Tables and Graph Theory.
Thanks for learning with the DigitalOcean Community. Check out our offerings for compute, storage, networking, and managed databases.

Get our biweekly newsletter
Sign up for Infrastructure as a Newsletter.

Hollie's Hub for Good
Working on improving health and education, reducing inequality, and spurring economic growth? We'd like to help.

Become a contributor
Get paid to write technical tutorials and select a tech-focused charity to receive a matching donation.


How can i change the STRUCT wich has a “children array” with 26 spaces to a STRUCT more efficient, talking about memory use?
- Lucas